In the world of Finite Element Analysis (FEA), symmetry serves as a powerful tool that can vastly improve the efficiency and speed of our calculations. Recognizing and leveraging symmetry within our models can potentially save us substantial computational resources and time.
Symmetry is utilized in FEA analysis to reduce computational efforts and time. By exploiting symmetric properties in a structure, only a portion of the model needs to be analyzed, reducing the mesh size and computations. It simplifies the analysis while still providing accurate results for the entire structure.
In this article, I will explain the crucial role of symmetry in FEA, elucidating why its consideration is paramount in the process of FEA. Drawing from my personal experiences and practical examples, I will explain how symmetry can enhance solving times, thus contributing significantly to the efficiency of our simulations.
What Is The Role Of Symmetry In FEA Analysis?
Symmetry in FEA plays a critical role in simplifying and speeding up calculations. When a model or component under analysis exhibits symmetry, it means that only a fraction of the total structure needs to be modelled and analyzed. This property is particularly useful in FEA as it significantly reduces the computational effort and resources needed to obtain accurate results.
A symmetrical model demands fewer elements or nodes, thus reducing the time taken for solution processes like meshing and solving.
Essentially, by harnessing the advantages of symmetry, engineers can achieve quicker and equally accurate FEA results, increasing overall productivity and efficiency.
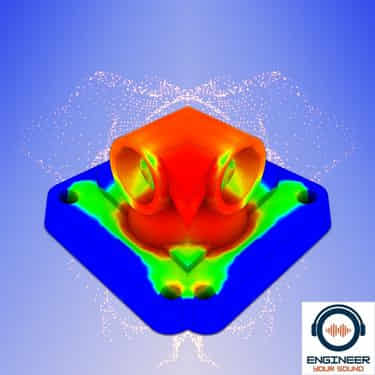
For example, in the following image, I can use symmetry planes and reflectivity to simplify the modelling of this orange brick. Modelling just 1/8, the geometry is symmetric about the symmetry planes. Therefore, my simulation package will “mirror” this geometry about the symmetry planes.
In essence, our model is much smaller than the original block size as it will require less processing time and elements, but the result will be as effective as if you modelled the entire block.

Why Do We Need To Consider Symmetry In FEA?
Symmetry needs to be considered in FEA for a variety of reasons. Primarily, it can dramatically reduce the computation load and time taken to solve problems. By analyzing only a portion of the model (which represents the whole due to symmetry), we can effectively cut down the number of elements in the mesh, decreasing computational demand and hastening the analysis process. This can be particularly beneficial in complex models and simulations, where computational resources can be a limiting factor.
Moreover, taking symmetry into account can also enhance the quality of the solution in terms of accuracy, as it can help reduce numerical errors that can accumulate during computations. It allows us to concentrate computational resources on a smaller area, thus affording a higher-resolution analysis of the model.
In a real-world context, symmetry also assures the consistency of results, making them more predictable and reliable. Hence, considering symmetry in FEA is critical for efficient, high-quality, and reliable modelling and analysis.
How Does Symmetry Improve Model Solve Times?
Symmetry significantly enhances model solve times by reducing the computational burden.
In a symmetric model, only a fraction of the entire structure is modelled and solved, which effectively decreases the number of elements in the mesh. This reduction leads to a decrease in the size of the mathematical problem that needs to be solved, resulting in quicker solution times.
Furthermore, less computational power is required, freeing up resources for other tasks or allowing for a higher resolution in the area of interest.
Hence, recognizing and utilizing symmetry in FEA can drastically enhance efficiency and productivity in the problem-solving process.
What Is An Example Of Symmetry In FEA Analysis?
A distinct example of symmetry in FEA analysis can be seen in the analysis of a car’s front suspension system. Due to the inherent design of the vehicle, the left and right sides of the suspension system are mirror images of each other, exhibiting perfect symmetry.
Consequently, it would be unnecessary to analyze the entire suspension system; instead, we can just model and analyze one side. This halves the computational effort, the mesh density, and the solve time, thereby increasing efficiency.
Notably, this approach would still yield an accurate representation of the entire suspension system’s performance under simulated conditions.
This example underscores the immense potential of utilizing symmetry in FEA analysis, demonstrating how it can significantly streamline the simulation process without compromising the accuracy of results.
What Are The Limitations Of Using Symmetry In FEA Analysis?
While the employment of symmetry in FEA analysis is a valuable strategy, it’s not without its limitations. The primary constraint is that symmetry can only be used when the model, load, and boundary conditions exhibit symmetric behaviour.
In real-world applications, perfect symmetry is rare, and even minor deviations can lead to inaccuracies in the results if not appropriately considered.
Another limitation is in modelling materials with a non-symmetrical response to loads, such as certain types of composites or materials exhibiting directional properties.
Using symmetry when completing modal analysis is not recommended as it will result in just the computing of just symmetrical modes. This is important as you may miss non-symmetric modes, which may be of interest.
Finally, the application of symmetry assumes that the solution will also exhibit symmetry, which may not always be the case, especially in nonlinear problems or when the structure’s response is influenced by factors not considered in the model. Hence, while symmetry can expedite the FEA process, it’s crucial to understand the nature of the structure, the loads, and the material properties to effectively and accurately apply this strategy.
What Is Cyclic Symmetry In FEA?
Cyclic symmetry, also known as periodic symmetry, refers to a special type of symmetry in FEA that is common in models with repeating patterns or features.
Instead of analyzing the entire model, you can analyze just one segment or sector and apply appropriate boundary conditions that reflect the repeating nature of the structure. This can significantly reduce the computational resources required, making it a highly effective strategy in FEA for models like turbine blades, gear teeth, or repetitive structures in civil engineering.
However, it’s worth noting that implementing cyclic symmetry requires careful consideration of boundary conditions and loading to ensure that the symmetry conditions are satisfied throughout the analysis.
Other Than Symmetry, How Can I Increase My Simulation Solve Times?
Aside from using symmetry, there are several other strategies that can be employed to increase simulation solve times in FEA.
- Mesh Refinement: Creating a mesh that accurately represents the geometry without unnecessarily increasing the number of elements can lead to faster solve times. The use of higher-order elements can also result in more accurate solutions, though it does increase computational load.
- Parallel Processing: If you have access to a multi-core processor or a computer cluster, you can distribute the computation load across multiple cores or nodes to speed up the analysis.
- Simplifying the Model: Where possible, simplifying the model by removing unnecessary features can reduce the size of the problem and, subsequently, the solving time.
- Appropriate Solver Selection: Different solvers are optimized for different types of problems. Selecting the solver that best fits your specific model can speed up solve times.
- Use of Submodelling: If you’re interested in a particular region of your model, you can create a detailed submodel of that region and connect it to a coarser model of the entire structure. This generally results in much faster solve times without significant loss in accuracy.
Remember, the goal is not just to decrease solve times but to do so in a way that maintains the integrity and accuracy of your results.
Final Thoughts
The use of symmetry in Finite Element Analysis (FEA) presents a potent approach to optimize computational resources, decrease solving times, and enhance efficiency.
However, the application of symmetry, be it simple symmetry or cyclic symmetry, requires an astute understanding of the model, load, and boundary conditions, as well as the intrinsic nature of structure and material properties.
While symmetry is a powerful tool, it is not without its limitations and should be used alongside other strategies like mesh refinement, parallel processing, model simplification, appropriate solver selection, and submodelling for the most efficacious results.
Ultimately, the key is to balance computational efficiency without compromising the accuracy and integrity of the results, ensuring reliable and robust solutions in FEA.
